Geographic coordinate conversion

Geographic coordinates consist of latitude and longitude.

Contents

Ways of writing coordinates

All of the following are valid and acceptable ways to write geographic coordinates:

Coordinates here are generally written as .

Basic forms

There are three basic forms of a coordinate.

  1. Coordinate containing degrees (integer), minutes (integer), and seconds (integer, or real number) (DMS).
  2. Coordinate containing degrees (integer) and minutes (real number) (MinDec).
  3. Coordinate containing only degrees (real number) (DegDec).

All forms of coordinates are capable of representing the same amount of data and the same precision. Depending on which type of coordinate you are provided with, and which type you would like to work with, you may have to do some conversion.

Components of a typical coordinate

In its most simple form a coordinate is just a number of degrees. The tricky part comes in when you need to differentiate North/South latitude or West/East longitude, or make the number more digestible by writing it with minutes and seconds instead of as a decimal number.

Degrees

The degrees portion of the coordinate is always going to be the easiest to figure out. The degrees is always the left-most whole number. For example:

40:26:46N         40
W87°43′41        -87

A sphere is divided into 360 degrees. The number space is divided into two halves, East and West in the case of longitude and North and South in the case of latitude. The maximum ranges are as follows:

Longitude
 180 W   = -180
 180 E   =  180

Latitude
  90 N   =   90
  90 S   =  -90

Technically you could have latitudes greater than 90 or less than -90, but this is an ambiguous case, since there would be an equivalent coordinate with an inverse longitude.

The minimal case is that you have only degrees:

 50.21389 or
 50.21389N

Minutes

Minutes are an optional component, as is implied by the minimal case of degrees. If there is no minutes component, the degrees component contains the entire precision of the coordinate and there must not be a seconds component. Minutes are actually the numerator component of a fraction with denominator 60 of one degree.

With the same examples as above:

40:26:46N         26
W87°43′41         43

In the first case, the number of minutes is 26.

Seconds

Seconds are also an optional component, and can only exist if the minutes component also exists. Seconds are the numerator component of a fraction with denominator 60 of one minute.

40:26:46N         46
W87°43′41         41

In the second case, the number of seconds is 41.

To convert, 41 seconds is equal to 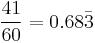\frac{41}{60} = 0.68\bar{3} minutes.

Putting it all together

Conversion from DMS to Decimal Degree

Given a DMS (Degrees, Minutes, Seconds) coordinate such as W87°43′41″, it's trivial to convert it to a number of decimal degrees using the following method:

  1. Calculate the total number of seconds:
    43′41″ = (43*60 + 41) = 2621 seconds.
  2. The fractional part is total number of seconds divided by 3600:
    2621 / 3600 = ~0.728056
  3. Add fractional degrees to whole degrees to produce the final result:
    87 + 0.728056 = 87.728056
  4. Since it is a West longitude coordinate, negate the result.
  5. The final result is -87.728056.

Conversion from MinDec to Decimal Degree

Given a MinDec(Degrees, Minutes, Decimal Minutes) coordinate such as 40°26.7717N, 79°56.93172W, it's trivial to convert it to a number of decimal degrees using the following method (for example for 79°56.93172W):

  1. The integer number of degrees is the same (79)
  2. The decimal degrees is the decimal minutes divided by 60 (56.93172/60 = 0.948862)
  3. Add the two together (79 + 0.948862 = 79.948862)
  4. Negate the value if it is South or West (in this case, West, so -79.948862)

Conversion from Decimal Degree to DMS

Given a decimal longitudinal coordinate such as -87.728055 it is trivial to convert it to DMS form. It will be necessary to know whether it is a latitudinal or longitudinal coordinate in order to fully convert it. The method is as follows:

  Type   Dir.   Sign    Test
  Lat.   N      +       > 0
  Lat.   S      -       < 0
  Long.  E      +       > 0
  Long.  W      -       < 0

A latitude of 0°0′0″ is neither North nor South. Similarly, a longitude of 0°0′0″ is neither East nor West. These are referred to as zero latitude or zero longitude.

Programmatical conversion

The most common programmatical use of these processes is to display a coordinate to an end user in the more common DMS form instead of decimal form. Below is a piece of pseudocode to convert from decimal degrees to degrees, minutes, and seconds:

function deg_to_dms ( degfloat )
   Input must be non-negative:
   if degfloat < 0
      error
   end if
   Compute degrees, minutes and seconds:
   deg ← integerpart ( degfloat )
   minfloat ← 60 * ( degfloat - deg )
   min ← integerpart ( minfloat )
   secfloat ← 60 * ( minfloat - min )
   Round seconds to desired accuracy:
   secfloat ← round( secfloat, digits )
   After rounding, the seconds might become 60. These two
   if-tests are not necessary if no rounding is done.
   if secfloat = 60
      min ← min + 1
      secfloat ← 0
   end if
   if min = 60
      deg ← deg + 1
      min ← 0
   end if
   Return output:
   return ( deg, min, secfloat )
end function

See also

External links